Police Car Chase: Catching The Speeder After Reaction Time - Explained

Andre Mitchell IV 23 May 2025

How long does it truly take for justice to catch up when speed and circumstance collide? The answer, as we'll discover, isn't always straightforward, and often hinges on the crucial seconds that define pursuit and capture.

The scenarios presented here explore a common drama: a police car attempting to apprehend a speeding vehicle. These situations offer a practical application of physics, specifically kinematicsthe study of motion. The core question in each case revolves around determining the time it takes for the pursuing police car to overtake the speeder, considering the officer's reaction time and the acceleration capabilities of the police vehicle.

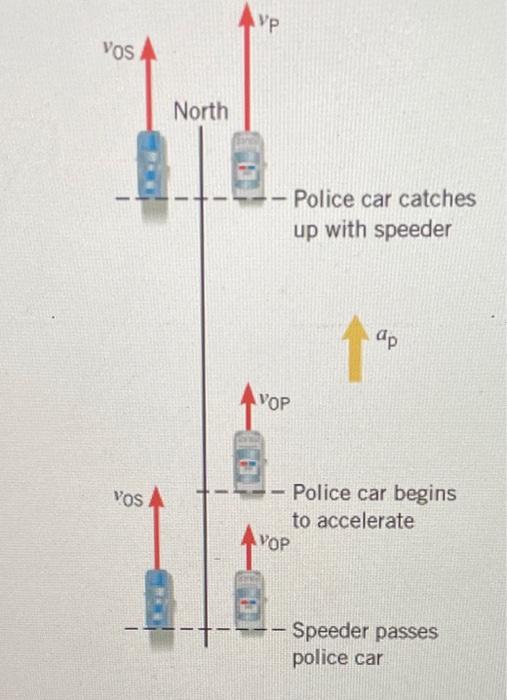
Consider the basic elements: A police car is traveling north, minding its own business, when a speeder, also headed north, zooms past. The police officer, upon recognizing the violation, initiates pursuit. There's a delay the reaction time before the officer hits the gas. Then, the police car accelerates, aiming to close the distance.

To solve these problems, we need to consider several factors. First, there's the speed of both vehicles. The speeder maintains a constant velocity, while the police car accelerates from its initial velocity (which might be zero, or it might be the car's existing velocity before pursuit begins). Second, the officer's reaction time introduces a crucial delay. The speeder gains distance during this reaction time. Third, the police car's acceleration determines how quickly it can increase its speed to match or surpass the speeder's.

Let's break down the essential concepts: Displacement refers to the change in an object's position. Velocity is the rate at which an object's position changes, and it has both magnitude (speed) and direction. Acceleration refers to the rate at which an object's velocity changes. In these police chase scenarios, we need to analyze how the displacement, velocity, and acceleration of the two vehicles interact.

One important aspect is the use of kinematic equations. These equations relate displacement, velocity, acceleration, and time. By applying these equations, we can formulate a mathematical model to predict when and where the police car will catch up with the speeder. The specific equations used will depend on the information provided in the problem and the assumptions we make. For instance, if we assume the speeder maintains a constant velocity and the police car accelerates at a constant rate, we can use a simplified set of equations.

For instance, let's analyze one example. A police car is traveling north at 18.0 m/s when a speeder passes it at 42.0 m/s. The officer reacts in 0.800 s and then begins to pursue with an acceleration of 5.00 m/s. To find the time it takes for the police car to catch up, we must take the following steps: Calculate the distance the speeder travels during the reaction time. Determine the time for the police car to cover the same distance. Then, apply kinematic equations to determine the time it takes for the police car to reach the speeder. A similar method can be applied for the other examples.

These problems aren't just hypothetical exercises; they mirror real-world situations. The dynamics of pursuit can be affected by various factors. Road conditions, traffic, and the speed differential between the vehicles can all impact the outcome. The reaction time of the officer is critical because the speeder will gain significant distance during the delay.

Another variation of the scenario could involve the initial velocity of the police car. The police car might not start from rest. It could already be traveling at a certain speed. A faster initial velocity will reduce the total time needed to catch the speeder. If the police car starts from rest, its acceleration becomes the most important factor in determining how quickly it can catch up to the speeder.

We are not limited to the north direction for these scenarios. These problems can also be adapted to horizontal motion or any other direction. The key is to consider the relative motion of the vehicles and how their velocities and accelerations change over time. The angle of the road is another factor to consider. The application of these calculations extends to real-world situations like accident investigations.

Radar guns are another layer to this situation. Police radar uses the Doppler effect to measure a car's velocity. The radar gun emits radio waves, which reflect off the moving car. The frequency of the reflected wave changes, depending on the car's speed. The radar unit calculates the car's velocity by measuring this frequency shift. The speed detected by radar is crucial information in these pursuit scenarios.

The pursuit, in this case, is based on simple physics principles. A police officer notices a car traveling at a velocity higher than the speed limit. After the officer's reaction time, the police officer steps on the accelerator. The speeder continues moving at a constant speed, and the police car accelerates to catch the speeder. The time it takes for the police car to catch up with the speeder can then be determined using kinematic equations.

The scenarios also highlight the importance of safety. The speeds involved can be dangerous, and officers must balance the urgency of the situation with the need to protect themselves and others. These calculations also allow us to consider how different acceleration rates, reaction times, and speed differentials influence the outcome of the chase.

Let's look at another problem. A police car is traveling at 15.0 m/s north, when a speeder zooms by at 45.0 m/s north. After a reaction time of 0.300 s, the officer pursues the speeder with an acceleration of 5.00 m/s. To determine how long it takes for the police car to catch up, we will use kinematic equations.

The use of kinematic equations allows us to predict how long it takes for the police car to overtake the speeder in various scenarios. By systematically applying these equations, we can gain a deeper understanding of the factors influencing pursuit outcomes.

The police cars response and performance are also critical factors. The acceleration of the police car is directly related to the time it takes to catch the speeder. The greater the acceleration, the faster the car can reach the speeder. In other words, the acceleration capability of the police car, along with the officers reaction time, is a key factor.

Furthermore, the initial velocity of the police car influences the chase's duration. If the police car is already moving, the pursuit becomes a race against time. The initial velocity must be factored into the calculations, as it affects the relative motion of both vehicles.

In these scenarios, the speed of the speeding car is another significant factor. The higher the speed, the more distance the speeder covers before the police car begins its pursuit. The speed differential between the two vehicles affects the overall time required to catch the speeder.

The pursuit problems demonstrate the principles of motion in action. They provide a practical context for understanding the concepts of displacement, velocity, acceleration, and time. The equations we use allows us to develop a deeper appreciation for the physics behind the motion of objects.

Here's another example: a police car at 18.0 m/s north, with a speeder at 48.0 m/s north. The reaction time is 0.500 s, and the police car's acceleration is 6.00 m/s. Including the reaction time, what is the total chase time? The approach remains the same calculate the distance covered by the speeder during the reaction time, and calculate the time it takes for the police car to match that distance.

These problems can also be viewed in the context of accident reconstruction. If the police car arrives at the scene, the time and location data, along with the police car's performance characteristics, might reveal the speed and the manner of operation of the speeding car.

In these scenarios, it's also important to note the limitations of these models. We are simplifying real-world situations. We may assume constant acceleration, which may not always be the case. The road conditions and factors can play a role in the outcome of the chase. Furthermore, other factors are the officers driving skills and decisions.

Let us briefly address the Doppler effect. Police radar uses the Doppler effect to determine a car's velocity. A stationary police car with a radar gun will detect a moving car's velocity. The same happens for a police car with a radar gun traveling toward the speeder. Thus, the Doppler effect is a critical tool for measuring speed in law enforcement.

In each situation, a series of calculations based on the fundamentals of kinematics, the reaction time, and the acceleration of the police vehicle, help determine the time required for a successful pursuit.

Consider a final example: an unmarked police car is at 95.0 km/h, passed by a speeder at 115 km/h. 2.50 s after the speeder goes by, the officer accelerates at 2.50 m/s. How much time passes? The approach we use in this scenario is again consistent.

These types of problems emphasize the practical application of the physics principles. They highlight the interplay between reaction time, acceleration, and velocity in pursuit scenarios. By learning these equations and applying them to these scenarios, we gain a deeper understanding of the physics of motion.

In each case, the goal is the same: to solve for the time it takes for the police car to catch up, integrating the factors involved: reaction time and acceleration. These calculations provide insights into the dynamics of law enforcement, and the principles of physics that influence the outcomes.

A police car is traveling at a velocity of 18.0 m / s due north, when a

Solved (III) An unmarked police car traveling a constant 95 Chegg

Solved A police car is traveling at a velocity of 17.0 m/s Chegg

Celebrity Relationships And Breakups

Police Car Chase: Catching The Speeder After Reaction Time - Explained

Detail Author:

Socials

facebook:

twitter:

tiktok:

instagram: