Master Percentages: Calculation Guide & Quick Tools!
Ever wondered how seemingly simple concepts like percentages can unlock a deeper understanding of the world around us? Percentages are fundamental to everything from personal finance to scientific analysis, offering a universal language for comparison and proportion.
The concept of percentage is ubiquitous, weaving its way into the fabric of everyday life. From understanding the discount on your favorite item during a sale to assessing the likelihood of a weather event, percentages provide a readily accessible way to interpret and compare different quantities. Calculating percentages empowers informed decision-making, enabling us to evaluate risks, track progress, and appreciate the relative significance of various factors. The utility of percentages extends far beyond basic arithmetic, serving as a cornerstone for advanced statistical modeling, economic analysis, and even creative fields like graphic design and data visualization.
A percentage is, at its core, a ratio expressed as a fraction of 100. The term "percent" itself originates from the Latin "per centum," meaning "out of one hundred." This foundational principle allows us to normalize disparate values, enabling direct comparisons. It offers a standardized framework for comparing values. Understanding this concept is crucial for interpreting data in a variety of contexts. For instance, a score of 6 out of 10 on a test translates to a 60% grade, which then communicates the proportion of correct answers relative to the total questions. By converting raw numbers into percentages, we gain a clear picture of how a particular value relates to the whole.
Consider the utility of a percentage increase calculator. This invaluable tool allows users to compute the increase or decrease of a specific percentage of an input number, streamlining calculations across various applications. The underlying principle revolves around converting the given percentage into its decimal equivalent. This is achieved by either subtracting (decrease) or adding (increase) the decimal equivalent from, or to, the base value. This seemingly simple process empowers us to efficiently analyze changes and trends in diverse fields. For instance, calculating a percentage increase in salary, where Mark's hourly wage rises from $15 to $18, becomes easily solvable using the percentage increase formula.
To illustrate, let's find the percentage value of 6 out of 8. By following these steps, we can easily find the percentage of 6/8:
- Express the given value as a fraction, in this case, 6/8.
- Multiply the fraction by 100%.
- So, (6 / 8) x 100% = (0.75) x 100% = 75%.
Therefore, 6 out of 8 equates to 75%.
- Explore Jaguar Dalgliesh Classics Crime Drama Discover Now
- Monster Basement Escape The Horror Puzzles Walkthroughs
Understanding how to convert a fraction into a percentage, involves a straightforward formula, allowing us to express fractions in terms of "per hundred." The process requires that you multiply the fraction by 100 and then add the percentage sign (%). For example, the fraction 6.5 / 10 can be converted into a percentage as follows: (6.5 / 10) 100 = 65%. Therefore, the fraction 6.5/10 is equal to 65%.
Another valuable aspect is to understand the percentage difference formula. This equation facilitates the calculation of the percentage difference between two values, offering insights into the magnitude of change. The formula involves taking the absolute value of the difference between two values, dividing that result by the average of those values, and then multiplying the outcome by 100. By using this method, one can determine the percentage change between two numbers, providing a standardized way to assess variations in diverse contexts.
One practical application involves understanding percentage increases in scenarios. For example, if Mark's hourly salary increases from $15 to $18, we can apply the percentage increase formula to determine the change:
- Calculate the increase: $18 - $15 = $3.
- Divide the increase by the original salary: $3 / $15 = 0.2.
- Multiply by 100 to get the percentage: 0.2 100 = 20%.
So, the percentage increase in Mark's salary is 20%.
When dealing with decimals, converting to percentages is as simple as moving the decimal point two places to the right. Consider the example that 2% translates to 0.02, and 50% equals 0.5. The ease of this conversion highlights the versatility of the percentage as a tool, making it easy to compare different values.
The percentage can also be conceptualized as a component within a larger algebraic equation. The basic formula can be expressed as: P v1 = v2. Here, P represents the percentage, v1 is the original value to be modified, and v2 is the resulting value after the percentage operation is applied. This formula is applicable in various situations, such as calculating the price after a discount, where the percentage (discount percentage) modifies the original price.
Consider a situation where you have 6.5 out of 10. This can be easily translated to a percentage with the following calculation: Divide 6.5 by 10, and multiply the result by 100. So, 6.5 / 10 x 100 = 65%. Thus, 6.5 out of 10 equates to 65%.
In the context of converting fractions, you divide the numerator by the denominator and then multiply the result by 100, adding the percent sign to complete the conversion. This method consistently converts fractions into their equivalent percentage forms, making it easy to compare values and analyze proportional relationships.
A percentage is also useful for understanding grades in class. For example, when evaluating test scores, a score of 6 out of 10 translates to a 60% percentage grade. In schools and universities, percentage grades often correspond to letter grades. For example, a 65% may be assigned a "D" letter grade, which is below average.
Let's say you want to calculate 15% of a $150 restaurant bill. By using the percentage formula, you calculate the result easily:
- Multiply the bill by 15%: $150 0.15 = $22.50.
So, 15% of $150 equals $22.50.
Now, consider the following scenario: you want to know what percentage 258 is of 457.2578. The formula is : (Part / Whole) 100. In this case, that would be (258 / 457.2578) 100 = 56.42%. This equation is a direct demonstration of how the percentage can be determined.
Furthermore, you can determine a percentage increase in Mark's hourly salary. If his initial salary is $15, and it's raised to $18. You can solve this problem using the percentage increase formula.
- Subtract the original salary from the new salary: $18 - $15 = $3
- Divide the increase by the original salary: $3 / $15 = 0.2
- Multiply by 100 to get the percentage: 0.2 100 = 20%
Therefore, the percentage increase in the salary is 20%.
To express the fraction 6.5/10 as a percentage, it is as simple as multiplying it by 100. This makes calculations easy, as shown by the following equation: (6.5 / 10) * 100 = 65%. Hence, 6.5 / 10 as a percent is 65%.
As the percentage symbol signifies, it means "out of one hundred." This symbol is widely recognized and used, often abbreviated as "pct" or "pc." A percentage is a convenient way to express a ratio or fraction. For instance, when you score 6 out of 10 in a class, assignment or class, you have a 60% percentage grade.
If you had an increase in the interest in your savings account from 2% to 3%, you could express this as an increase of 50% of the old interest rate, or as an increase of 1 percentage point (which is 1% of the whole). This example demonstrates how to express changes using percentages.
Using a percentage calculator is a straightforward process. Start by entering the numbers relevant to your calculation, such as the total amount and the percentage you're calculating. Then, choose the specific percentage operation you need, like percentage increase, decrease, or proportion. The calculator will automatically work out the answer for you. Just type into the box and then hit the calculate button.
Consider the scenario: what is 10% of 100? You would compute this by multiplying 100 by 0.10. That would be 10. If you want to understand what the 100 is in relation to 110, you see that 100 to 110 is a 10% increase, but to go from 110 back down to 100 is a 9.09% decrease. This showcases how percentages can be applied in a variety of contexts.
In mathematics, a percentage is a dimensionless number. It is a ratio or a number that is expressed as a fraction of 100. The symbol used to denote percentage is the percentage sign (%). The percentage is used to express the proportionate part of the total number. Therefore, the percentage is a dimensionless number.

Convert Fraction to Percent
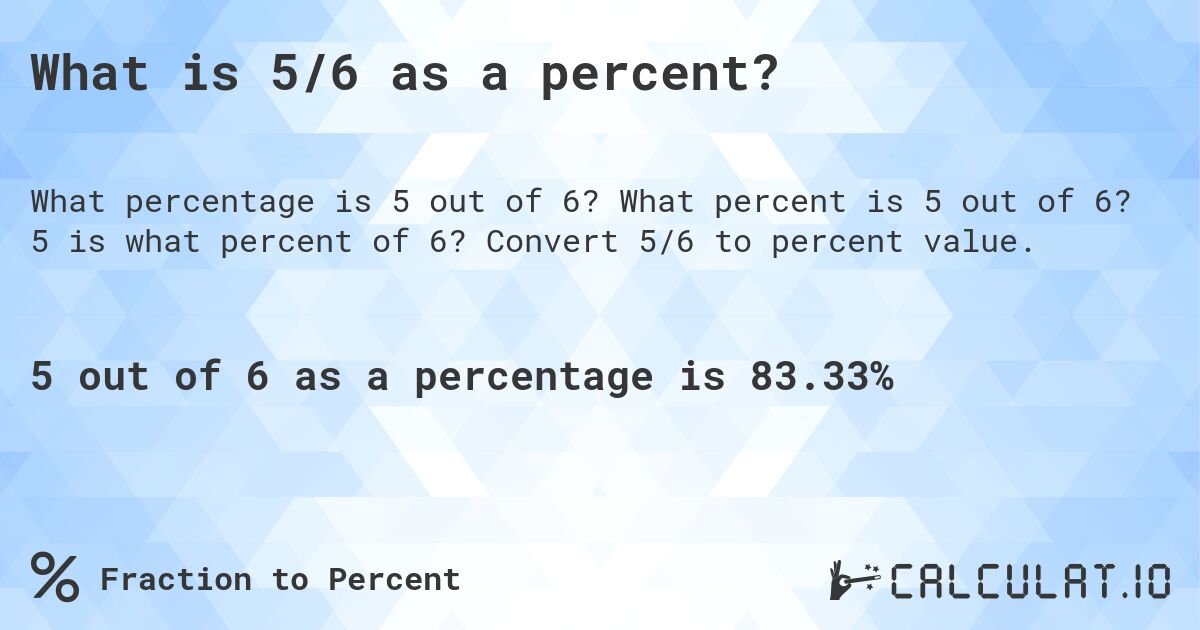
What is 5/6 as a percent? Calculatio
Fractions, Decimals, and Percents Chart CTP4330 Creative Teaching